體育博彩的歷史可追溯至古希臘和羅馬時代,這種娛樂活動在人類文明中有著深厚的根基。隨著北美多個地區在線體育博彩合法化,全球博彩市場預計在2028年將達到驚人的1400億美元規模。這一巨大的經濟潛力不僅吸引了投資者的目光,也引起了學術界的廣泛關注。體育博彩市場的效率問題一直是研究的熱點,儘管多項研究報告指出市場存在低效現象,但也有相反的結論出現,這種分歧可能意味著效率低下的情況在不同體育市場中存在差異。
深入研究體育博彩不僅揭示了”群眾智慧”(Wisdom of the Crowd)的應用價值,還展示了市場價格的預測能力,以及定量評級系統(Quantitative Rating Systems)在預測中的重要性。特別值得注意的是,研究發現博彩公司能夠巧妙地利用公眾偏見(Public Biases)來最大化其利潤,這一發現對理解博彩市場的運作機制至關重要。
在博彩理論的發展中,Kelly準則(Kelly Criterion)提供了優化投注額大小的理論基礎,這一理論可直接應用於體育博彩。Hvattum和Arntzen的研究進一步評估了Kelly投注策略及兩種啟發式投注策略(Heuristic Betting Strategies)的效果,為投注者提供了更多實用的指導。
北美市場中最受歡迎的體育博彩形式之一是”點差投注”(Point Spread Betting),投注者需要預測比賽的勝差是否會超過博彩公司設定的數值。這種投注形式引入了一個關鍵概念:勝差(Margin of Victory),定義為主隊得分與客隊得分之差。為了進行理論分析,我們將勝差m建模為一個連續的隨機變量,其累積分佈函數(Cumulative Distribution Function, CDF)表示為F(x) = P(m < x)。博彩公司設定的點差s則可視為對m的估計。
在點差投注中,”覆蓋點差”(Cover the Spread)和”贏點差”(Beat the Spread)是兩個關鍵術語。當s為正(主隊被看好)時,如果m > s,則稱主隊覆蓋點差;反之,如果s為負(客隊被看好),且m < s,則稱客隊覆蓋點差。這種機制增加了博彩的複雜性和吸引力。
本研究提出了一系列重要定理,為體育博彩的最優決策提供了理論基礎。定理1指出,為了最大化投注的期望收益,應當在且僅在點差小於m的τ分位數時投注主隊。這一結果的重要性在於,它表明最優投注決策不需要完全了解m的分佈,只需知道其特定分位數即可。
定理2進一步闡明了獲得正期望收益的條件,即只有當點差小於m的τ分位數或大於m的(1-τ)分位數時,才有可能實現正收益。這一發現與文獻中描述的”無利可圖投注區域”(No-Arbitrage Betting Zone)概念相呼應,為投注者提供了明確的決策指導。
在實際應用中,估計勝差m是關鍵。定理3和定理4分別界定了投注錯誤和超額錯誤的概率界限,這為評估投注策略的效果提供了理論依據。特別是,定理4指出,滿足F(m̂) = F(s)的任何估計量都能最小化超額錯誤的概率,這一結果對於開發最優預測模型具有重要意義。
本研究還探討了”單次投注”(Moneyline Betting)和”大小投注”(Over-Under Betting)的最優策略,通過一系列推論擴展了理論框架的適用範圍。值得注意的是,Moneyline投注的最優決策需要了解接近0或1的分位數,這對預測模型提出了更高的要求。
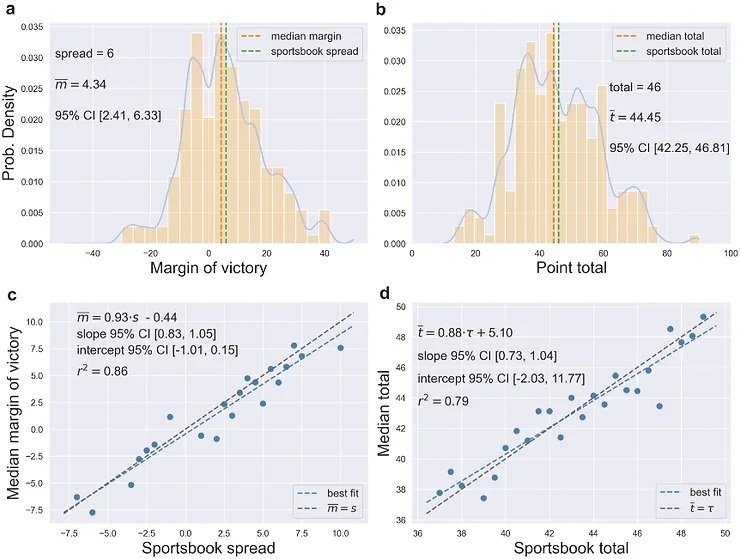
為了驗證理論結果,本研究對國家美式足球聯盟(NFL)的大量歷史數據進行了實證分析。結果顯示,博彩公司的點差和總分預測分別解釋了實際結果86%和79%的變異性,這表明博彩公司的預測具有很高的準確度。然而,研究也發現,博彩公司的預測偏離真實中位數僅1點,就可能為投注者帶來正的期望收益,這凸顯了精確預測的重要性。
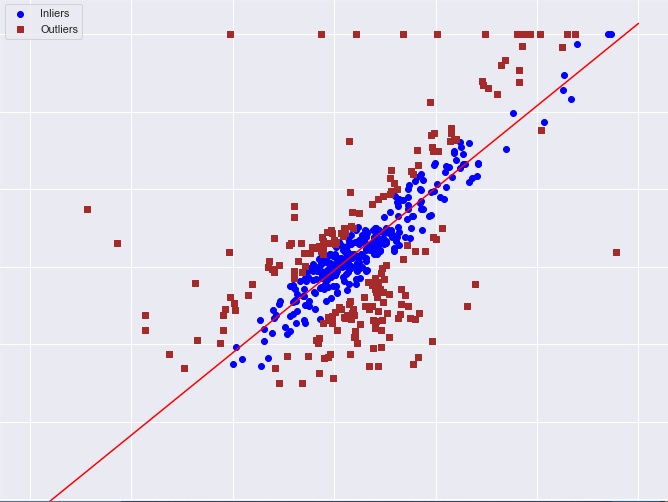
本研究的一個重要貢獻是提出了使用分位數回歸(Quantile Regression)而非傳統普通最小二乘回歸(Ordinary Least Squares Regression)進行體育博彩建模的建議。分位數回歸能更好地捕捉結果變量的分佈特征,特別是在存在異常值或多峰分佈的情況下。
最後,本研究討論了體育博彩中的偏差-方差權衡(Bias-Variance Trade-off)問題。有趣的是,研究發現在某些情況下,具有較大偏差但低方差的模型可能比高精度低穩定性的模型更有優勢。這一發現對於開發實用的體育博彩預測模型具有重要的指導意義。
總結來說,本研究不僅深化了我們對體育博彩市場的理解,還為投注者和研究者提供了一個堅實的理論框架。通過結合先進的統計方法和大量的實證數據,本研究為體育博彩領域的未來研究指明了方向,同時也為投注者制定更明智的決策策略提供了科學依據。
Paper原文連結 : https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0287601